t'as pas fini.t'as oublié les arabes...
Annonce
Réduire
Aucune annonce.
De grands mathématiciens et de leurs biographie.
Réduire
X
-
Revenons aux deux français Laplace et Poincaré et à Lagrange qui lui était plutot Italien.
Joseph-Louis Lagrange
Joseph Louis, comte de Lagrange (Giuseppe Lodovico Lagrange en italien) (25 janvier 1736, Turin - 10 avril 1813, Paris) est un mathématicien et astronome italien.

Sa vie
Nommé très jeune professeur à l’école d’artillerie de Turin en 1755, il y fonde en 1758 l’Académie de Turin qui publie ses premiers travaux. Il est admis à l’Académie de Berlin par Euler, à qui il succède comme président. Transféré à Paris, où il avait fait publier sa Mécanique analytique (1787), peu avant la Révolution française, il doit à son génie d’échapper aux mesures de répression contre les étrangers. Des arrêtés spéciaux du Comité de salut public lui permettent de continuer d’exercer ses fonctions.
Surtout connu pour avoir introduit la méthode analytique en géométrie, il n’en a pas moins étudié toutes les branches des mathématiques et a laissé d’importants travaux tant en géométrie qu’en trigonométrie et en mécanique.
L’astéroïde (1006) Lagrangea a été nommé en son honneur.
Ses œuvres
Lagrange est probablement un des plus grands scientifiques du XVIIIe siècle.
Œuvres écrites
Il a publié un mémoire Réflexions sur la résolution algébrique (1771) qui a inspiré Abel et Galois, et la Mécanique analytique (1787), une version digitalisée se trouve p.e. ici Oeuvres de Lagrange, edition par Joseph Alfred Serret, Paris 1867 (Mécanique analytique voyez volumes 11 et 12.)
Théorie
Fondateur du calcul des variations avec Euler et de la théorie des formes quadratiques, il démontre le théorème de Wilson sur les nombres premiers et le théorème de Bachet sur la décomposition d’un entier en quatre carrés. Son nom figure partout en mathématiques. On lui doit le théorème de Lagrange sur la théorie des groupes, un autre sur les fractions continues, l’équation différentielle de Lagrange, la fonction de Lagrange ainsi que les équations de Lagrange en mécanique analytique.
Lagrange entreprend aussi des recherches importantes sur le problème des trois corps.
Commentaire
-
Pierre-Simon Laplace
Pierre-Simon Laplace, né le 23 mars 1749 à Beaumont-en-Auge (Calvados), mort le 5 mars 1827 à Paris, était un mathématicien, astronome et physicien français particulièrement célèbre par son ouvrage en cinq volumes Mécanique Céleste

Biographie
Après avoir terminé ses études à l'université de Caen, il rencontra d'Alembert, reconnu à l'époque pour ses études d'astronomie physique (mouvement et tables de la lune ; précession des équinoxes ; travaux sur la cause des marées, la dynamique etc.) et de mathématiques (développement du calcul intégral et différentiel ; dérivées partielles...) ainsi que pour sa participation avec Diderot à la mise en œuvre de l'encyclopédie. D'Alembert reconnut très rapidement le talent de Laplace, l'encourageant dans ses recherches. Ce dernier fut d'ailleurs nommé professeur de mathématiques à l'École militaire - poste peu exigeant qui lui laissait le temps de développer ses propres études.
Laplace fut l'un des premiers savants à s'intéresser de très près à la question de la stabilité à long terme du système solaire. La complexité des interactions gravitationnelles entre le Soleil et les planètes connues à l'époque ne semblaient pas admettre une solution analytique simple. Newton avait d'ailleurs déjà pressenti ce problème après avoir remarqué certaines irrégularités dans le mouvement de certaines planètes. Cependant, ce dernier en déduisit qu'une intervention divine était nécessaire de manière à éviter la dislocation du système solaire.
Laplace a également développé la théorie des probabilités dans Essai philosophique sur les probabilités (1814 : ses premiers travaux sur les probabilités ont commencé entre 1771 et 1774, notamment la redécouverte après Bayes des probabilités inverses, dites Loi de Bayes-Laplace, ancêtre des statistiques inférentielles.). Il fut le premier à publier la valeur de l'intégrale de Gauss. Il étudia la transformée de Laplace bien que Heaviside développa ce procédé de manière complète. Il adhéra à la théorie de Lavoisier avec qui il détermina les températures spécifiques de plusieurs substances à l'aide d'un calorimètre de sa propre facture.
Il devient en 1821 le premier président de la société de géographie lors de sa fondation.
Laplace est aussi connu pour sa conception d'un démon (ou démon de Laplace) capable de connaître, à un instant donné, tous les paramètres de toutes les particules de l'univers. Dans cette perspective, l'auteur adopte une position déterministe, soit une position philosophique et scientifique capable d'inférer de ce qui est, ce qui doit être. Ce concept de démon sera notamment remis en cause par le principe d'incertitude d'Heisenberg.
Œuvres de Laplace
Textes de vulgarisation
* Pierre-Simon Laplace ; Exposition du système du monde, Bachelier (Paris : 1836). Réédité dans la collection Corpus des oeuvres de philosophie en langue française, Fayard (1984), ISBN 2213014779. Texte complet disponible sur Gallica.
Textes techniques
* Pierre-Simon Laplace ; Oeuvres complètes de Laplace, publiées sous les auspices de l'Académie des sciences par MM. les secrétaires perpétuels, Gauthier-Villars (Paris : 1878-1912), 14 vol. Comprend : I-V. Traité de mécanique céleste ; VI. Exposition du sytème du monde ; VII. 1-2. Théorie analytique des probabilités ; VIII-XII. Mémoires extraits des recueils de l'Académie des sciences de Paris et de la classe des sciences mathématiques et physiques de l'Institut de France ; XIII-XIV. Mémoires divers.
* Pierre-Simon Laplace ; Théorie analytique des probabilités, Tome VII des oeuvres complètes (Paris - 3e édition - 1820).Dernière modification par Invité, 20 août 2006, 23h32.
Commentaire
-
Henri Poincaré
(wikipedia)
Henri Poincaré, né le 29 avril 1854 à Nancy et décédé à Paris le 17 juillet 1912, est un mathématicien et physicien français. Artisan de génie, il est l'homme de l'ombre de la relativité générale. En relation avec un physicien expérimental, Hendrik Antoon Lorentz, il met en équation la théorie de la relativité restreinte, sur les observations de son collègue.

Arrière petit fils d'Étienne Geoffroy Saint-Hilaire, il est le cousin de l'homme politique et président de la France Raymond Poincaré et de Lucien Poincaré, directeur de l'Enseignement secondaire au Ministère de l'Instruction publique et des Beaux-Arts. Brillant élève, il passe successivement par Polytechnique puis l'École des Mines; en 1879 il obtient un doctorat de mathématiques sous la direction de Charles Hermite, puis est détaché à la Faculté des Sciences de Caen. Deux ans plus tard, il obtient ses premiers résultats marquants en mathématiques (sur la représentation des courbes et sur les équations différentielles linéaires à coefficients algébriques), et rapidement, il s'intéresse à l'application de ses connaissances mathématiques en physique et plus particulièrement en Mécanique. Il occupera notamment la chaire de mécanique physique et expérimentale en 1885, la chaire de Physique Mathématique et de Calcul des probabilités de la Faculté des Sciences de Paris en 1886, succèdant à Gabriel Lippmann, puis en 1896 la chaire d'Astronomie mathématique, succédant à Félix Tisserand. C'est Joseph Boussinesq qui le remplacera ensuite à la chaire de physique mathématique. Il est en 1901 le premier lauréat de la Médaille Sylvester de la Royal Society. Il a été président de la Société mathématique de France en 1886 et en 1900 et président de la Société française de physique en 1902.
Poincaré est le fondateur de la topologie algébrique. Ses principaux travaux mathématiques ont eu pour objet la géométrie algébrique, des types de fonctions particuliers – les fonctions dites « automorphes » (il découvre les fonctions fuschiennes et kleinéennes), les équations différentielles... La notion de Continuité est centrale dans son travail, autant pour ses répercussions théoriques que pour les problèmes topologiques qu'elle entraîne.
Poincaré s'est intéressé tout au long de sa carrière d'enseignant aux nouvelles théories présentées par ses collègues mathématiciens et physiciens – ainsi, en physique, il s'occupa principalement d'optique et de la théorie électromagnétique de la lumière. Pour l'ensemble de ses travaux, Poincaré fut pressenti douze fois au prix Nobel de Physique; toutefois, sa faible activité expérimentale et la précocité de ses théories par rapport à la Relativité nouvelle telle que formulée en 1905, firent qu'il n'obtint jamais le prix.
Poincaré et la relativité restreinte
En 1905, Poincaré a trouvé dans les équations de transformation de Lorentz les bases de la théorie de la relativité dite restreinte. Poincaré a réformulé les transformations de Lorentz, les mettant dans leur forme classique qui est employée dans tous les livres universitaires encore aujourd'hui. Le 5 juin 1905, dans une note à l'Académie des Sciences de Paris, Poincaré a présenté sa découverte des transformations de vitesse, qui manquaient à Lorentz, ce qui a permis à Poincaré d'obtenir l'invariance parfaite, le dernier pas dans la découverte de la théorie de la relativité dite restreinte. La théorie dite restreinte prend une importance additionnelle unique quand on considère que la théorie dite générale de la relativité n'est qu'une théorie de la gravité. La théorie dite restreinte est alors la seule et unique théorie de la relativité.
Poincaré et le problème des trois corps
Poincaré est également l'inventeur de l'attracteur étrange, la solution à l'insoluble problème des trois corps : il trouva que trois corps obéissant à la gravitation universelle de Newton ont, sous certaines conditions, une trajectoire qui dépend fortement de la condition initiale. Ainsi, aucun homme ne pourra jamais déterminer avec exactitude le destin de ces corps, car la moindre perturbation dans ses mesures entraînerait irrémédiablement une forte différence de trajectoire. Ces supputations sont à l'origine de la théorie du chaos.
Mathématicien et philosophe
Il est aussi le dernier à avoir la double spécificité de comprendre l'ensemble des mathématiques de son époque et d'être en même temps un penseur philosophique. On le considère comme un des derniers grands savants universels, du fait de ses recherches dans des domaines transversaux (physique, optique, astronomie...), et de son attitude scientifique fondée sur une esthétique de la science et du nombre, à rapprocher de celle des Anciens grecs. Poincaré a œuvré toute sa carrière durant à la vulgarisation de ses résultats et des grands travaux de la science, attitude qui sera reprise par des physiciens ultérieurs comme Albert Einstein ou Stephen Hawking. Avec La science et l'hypothèse, Poincaré avait intéressé le monde artistique, notamment les cubistes, et donné des clés de compréhension aux géométries non-euclidienne.
Les études légendaires de Henri Poincaré
De façon plus anecdotique, il détient jusqu'à maintenant le record de la moyenne des notes obtenues au concours d'entrée à l'École polytechnique. Il rentra major, et en sortit deuxième.
Concernant son admission à l'École polytechnique, il existe une légende, selon laquelle il aurait été le seul étudiant à y avoir été admis alors qu'il avait obtenu un zéro à une épreuve (lavis), ce qui constitue normalement une note éliminatoire. Ce qui aurait penché en sa faveur serait le fait qu'il ait obtenu la note maximale, soit 20/20, à toutes les autres épreuves. Le jury d'admission aurait été partagé entre le fait de se priver d'un élément aussi brillant que lui, et l'application de la règle du zéro éliminatoire. Cette entorse au règlement demeurerait unique dans l'histoire de l'École. La réalité rejoint presque la fiction : il avait eu en fait 1/20 en dessin (lavis), 20 /20 aux trois epreuves de Mathematiques et 19 en Physique.
Il reçoit la médaille d'or de la Royal Astronomical Society en 1900.
Commentaire
-
Ibn Al-Haytham
Ibn al-Haytham dit Alhazen (Bassorah 965 - Le Caire 1039) est un mathématicien, physicien et philosophe arabo-islamique.

Il est célèbre pour avoir écrit :
- le Traité des courbes géométriques ;
- mais surtout Les Trésors de l'optique (Kitab al-Manazir) où à l'inverse d'Euclide puis de Ptolémée, il distingue vision et éclairement lumineux et affirme que la lumière part de l'objet vers l'œil dont la position du cristallin détermine l'image qui sera perçue.
il est aussi consideré comme le plus grand physicien de l'Islam, Ibn al-Haytham, connu par l'Occident médiéval sous le nom d'Alhazen, naît en Irak en 965. Il se rend au Caire sous le règne du calife fatimide Al-Hakim dont la bibliothèque est alors presque aussi remarquable que celle de la Maison de la Sagesse de Bagdad. Mais la carrière d'Ibn al-Haytham au Caire ne tourne pas comme il le souhaite. Soutenant que les inondations du Nil sont dues à un défaut de contrôle hydraulique, il obtient le financement du calife pour une expédition technique en Haute Egypte, vers la source du Nil. Parvenu à la première cataracte, Ibn al-Haytham doit cependant admettre que son projet est irréalisable. De retour après cet échec, on lui confie un petit poste dans le gouvernement, mais Ibn al-Haytham craint que le calife, excentrique et sanguinaire, ne le châtie. Pour échapper à la colère du Prince, il choisit de feindre la folie. Il ne recouvrira la santé mentale qu'à la mort d'Al-Hakim. Enfin libre de ses mouvements alors qu'il approche tout de même la soixantaine, Ibn al-Haytham peut enfin se consacrer entièrement à ses travaux scientifiques.
L'œuvre d'Ibn al-Haytham recouvre plus d'une centaine d'ouvrages dans les domaines des mathématiques, astronomie, physique et même philosophie. Ses apports ont été particulièrement importants en optique où il obtint des résultats totalement nouveaux, en rupture avec les théories grecques. Dans son livre Kittab al manadir (le Livre de l'optique), référence pour toute la physique du Moyen Age, Ibn al-Haytham expose ses théories sur la vision et la lumière. Il étudie avec précision l'anatomie de l'œil et établit que les rayons lumineux se dirigent en ligne droite de l'objet vers l'œil et non le contraire. Il observe également les phénomènes de réfraction et diffraction de la lumière. En astronomie comme en mathématiques, Ibn al-Haytham reprend et améliore les théories de ces prédécesseurs. Ses méthodes de travail, particulièrement modernes puisqu'il adopte une approche mathématique et expérimentale des problèmes, ont fait de son œuvre l'apogée de la physique arabe.
infoscience.fr
Commentaire
-
Al-Khuwārizmī

Timbre soviétique commémorant le 1200ème anniversaire de Muhammad al‑Khwarizmi en 1983.
Muhammad ibn Mūsā al-Khuwārizmī محمد بن موسى خوارزمي né vers 783 à Khiva dans le Khwarezm qui a donné son nom, décédé vers 850 à Bagdad), mathématicien Perse, est l'auteur de l'ouvrage intitulé Al-ĵabr wa'l-muqābalah الجبر و المقابلة qui signifie « La transposition et la réduction » publié en 825. Le terme al-jabr fut repris par les Européens et devint plus tard le mot algèbre. Son autre ouvrage, disparu, Kitāb 'al-ĵāmi` wa'l-tafrīq bī h'isāb ’al-Hind كتاب الجامع و التفريق بحساب الهند - « Livre de l'addition et de la soustraction d'après le calcul indien » est le premier à parler du système des chiffres indiens.
Le livre contient six courts chapitres, consacré chacun à un type particulier d'équation. Il ne contient aucun chiffre. Toutes les équations sont exprimées avec des mots. Le carré de l'inconnue est nommé «le carré» ou mâl, l'inconnue est «la chose» ou shay ou jidhr, la constante est le dirham ou adǎd.
Son nom, al-Khuwārizmī, latinisé au Moyen Âge en Algoritmi, puis en Algorisme par les Européens, est à l'origine du mot algorithme, qui veut dire « procédure ». En revanche le principe des algorithmes était connu depuis l'Antiquité (algorithme d'Euclide), et Donald Knuth mentionne même leur usage par les Babyloniens.
De manière anecdotique, on doit aussi à ’al-Khuwārizmī la tradition consistant à appeler l'inconnue d'une équation mathématique X. En effet, dans son ouvrage ’Al-ĵabr wa'l-muqābala, il expose une méthode (un algorithme au sens propre, donc) pour expliciter une inconnue, ou šay', littéralement « chose », dans une équation du premier degré, en utilisant des ĵabr, « soustractions » (ou « transpositions ») et des muqābala, « égalités » (ou confrontation de deux entités). Après plusieurs avatars, šay ’ (écrit xay en espagnol ancien) a fini par donner X.
Origine du mot Algèbre
Le mot algèbre vient du titre d'un livre, al-jabr wa'l muqabalah, écrit par al-Khwarizmi
Ce livre est dédié au calife al-Mamoun qui régne à Bagdad de 813 à 833 (après son père, le célèbre calife, Haroun al-Rashid, qui régna de 786 à 809, et après une guerre de succesion qui se termine par l'assassinat de son frère aîné en 813).
La traduction habituelle du mot jabr est restauration, et dans ce cas précis, il indique le passage d'un terme d'une équation de l'autre côté du signe égal. Par exemple, on fait une "jabr" quand on transforme y + 4 = x en y = x - 4.
Le mot muqabalah est traduit par confrontation ou réduction, et dans ce cas précis, il désigne l'opération consistant à éliminer les termes identiques et opposés dans une équation. Par exemple, on fait une "muqabalah", quand on transforme y + 3 = x + 3 en y = x, ou lorsqu'on transforme a + y - a = x en y = x.
Contenu du livre al-jabr wa'l muqabalah
Le livre contient six courts chapitres, chacun consacré à un type particulier d'équation.
Le livre ne contient aucun chiffre. Toutes les équations sont exprimées avec des mots. Le carré de l'inconnue est nommé le carré ou mãl, l'inconnue est la chose ou shay ou jidhr, la constante est le dirham ou adãd.
Les six formes canoniques sont :
ax2 = bx
ax2 = c
bx = c
ax2 + bx = c
ax2 + c = bx
ax2 = bx + c
Les autres formes ne sont pas traitées car elles n'ont pas de racine positive.
Le premier chapitre est illustré avec les trois exemples suivants : x2 = 5x ; x2 / 3 = 4x ; 5x2 = 10x.
Les deuxième et troisième chapitres sont illustrés, chacun avec trois exemples (que je ne connais pas).
Le quatrième chapitre est illustré avec les trois exemples suivants : x2 + 10x = 39 ; 2x2 + 10x = 48 ; (1/2)x2 + 5x = 28.
Le cinquième chapitre est illustré avec un seul exemple : x2 + 21 = 10x.
Le sixième chapitre est illustré avec un seul exemple : 3x + 4 = x2.
Les algébristes musulmans
La bait al-hikma (maison de la sagesse) est créée à Bagdad à l'époque du calife al-Mamoun qui régne de 813 à 833. Cette académie des sciences perdure sous les califats suivants d'al-Mu'tasim (833-842), al-Wathiq (842-847), al-Mutawakkil, etc. Elle cesse d'exister avec l'effondrement des abassides (prise et destruction de Bagdad en 1258).
al-Khowarizmi (c. 780-c. 850) travaille dans cette académie et est l'auteur du premier livre d'algèbre.
abd al Hamid ibn-Turk est l'auteur d'un manuscrit ressemblant à celui al-Khwarizmi, qui est, peut-être, un peu plus ancient.
al-Hajjaj ibn Yusuf ibn Matar (9e siècle), membre de la bait al-hikma, est le premier traducteur arabe d'Euclide.
al-Mahani (c. 820-880) est un astronome perse, mort à Bagdad. Il commente le livre 10 d'Euclide et commence l'étude du problème d'Archimède selon lequel le rapport du segment AE à un segment gamma est égal au rapport d'une aire delta au carré du segment EB ou (AE / gamma) = (delta / EB), ou encore ((a - x) / gamma) = (delta / x2).
Thabit ibn Qurrah (826-901) est issu d'une famille riche qui fait partie des Sabians, une communauté d'origine greque vivant à Harran en Turquie. Il devient astronome à Bagdad. Il traduit en arabe Euclide, Archimède, et Apollonius. Son fils Sinan (c. 880-943) est un grand médecin et un bon mathématicien. Son petit-fils Ibrahim (908-946) est un bon géomètre.
abu-Kamil Shoja ben-Aslam ou abu Kamil Shuja Ibn Aslam (c. 850-c. 930), probablement d'origine égyptienne, déclare qu'al-Khwarizmi est l'inventeur de l'algèbre. Il connait l'arithmétique de Diophante. Il est l'auteur d'un livre contenant 69 problèmes d'algèbre dont plusieurs ont des inconnues élevées à des puissances supérieures à trois.
abu al-Jud (10e siècle) étudie les coniques.
al-Khazin (c. 900-c. 971) est un astronome perse. Il étudie l'intersection de deux coniques.
Mohammad abu'l-Wafa al-Buzjani (940-998) est un astronome perse qui vient travailler à Bagdad au service du calife Adud ad-Dawlah qui régne de 949 à 983. Il est l'un des rares musulmans à s'intéresser aux nombres négatifs, probablement parce qu'il utilise l'algèbre pour des problèmes de comptabilité (dont les dettes) et pas seulement pour des problèmes de géométrie.
al-Quhi (c. 940-c. 1000) est un perse qui se voit confié la direction de l'observatoire astronomique de Bagdad fondé par le calife Sharaf ad-Dawlah (fils d'Adud ad-Dawlah) en 988. Il invente un compas spécial pour tracer des coniques. Il étudie l'intersection de deux coniques. Il se sert des moyennes proportionnelles pour transformer un solide en un cube. Il montre que I décrit une parabole dans l'équation AD x C = ID2. Il montre que I décrit une hyperbole dans l'équation ID x DB = C2.
ibn al-Haitham, alias, al-Basri, alias Alhazen (c. 965-1039), est un ingénieur, né à Basra en Iraq. Il s'installe au Caire en Egypte au service du calife al-Hakim. célèbre pour ses travaux en optique.
al-Karaji, alias al-Karkhi (953-1029) vit à Bagdad. Il connait l'arithmétique de Diophante. Il trouve la formule xmxn = xm+n et s'en sert pour trouver les racines carrés de la forme xmynzp.
Il est l'auteur de deux livres d'algèbre, al fakhri et al badir, et un livre d'arithmétique, al kafi.
Parmi ses exemples se trouve la division du polynome 6x8 + 28x7 + 6x6 - 80x5 + 38x4 + 92x3 - 200x2 + 20x par le polynome 2x5 + 8x4 - 20x.
Sinan ibn al-Fath résoud des problèmes en x9 et étudie l'équation x2n+p + bxn+p + cxp = 0.
Omar al-Khayyam (c. 1044-1123 ou 1048-1131), est un poète et mathématicien perse qui vit à Nishapur et à Samarkand. Il définit 25 types d'équation. Il rend les équations homogènes en utilisant 12 et 13. Pour résoudre les équations du troisième degré, il cherche à les décomposer en deux équations de coniques. Il utilise la méthode de l'insertion des moyennes proportionnelles.
al-Samawal (c. 1130-1174) est le fils d'un juif marocain. Il est né à Bagdad. Il voyage au moyen orient et se convertit à l'islam. Il reprend et continue les travaux d'abu Kamil et d'al-Karaji. Il utilise un raisonnement par induction. Il s'oppose à l'astrologie des voyants.
Sharaf al-Din al-Tusi (c. 1135-1213) (à ne pas confondre avec Nasir al-Tusi) est un mathématicien perse qui enseigne en Syrie et en Iraq. Il reprend les travaux d'al-Karaji et étudie le point d'intersection de deux coniques. Il résoud des équations du troisième degré par une méthode itérative. Il reprend le problème d'Archimède et d'al-Mahani, et réussit à trouver la valeur maximale du segment AE dans (AE / gamma) = (delta / EB) en annulant la dérivée.
Jamshid al-Kashi (c. 1380-1429 ou 1436) est un astronome perse qui vient travailler à la madrasah (école) de Samarkand, en Ouzbekistan, fondée en 1420 par le prince mongol Ulugh Beg, petit-fis de Tamerlan. Il continue les travaux d'al-Karaji, al-Samawal, et al-Tusi. Il se sert d'une méthode itérative pour trouver les valeurs approchées des racines sixièmes et de pi. Il est l'un des derniers mathématiciens musulmans.
Il y a d'autres mathématiciens musulmans connus mais ils font moins d'algèbre :
* al-Kindi (801-873), riche arabe, membre de la bait al-hikma, philosophe, arithméticien, et géomètre.
* Hunayn ibn Ishaq (808-873), chrétien nestorien, membre de la bait al-hikma, traducteur de Platon et d'Aristote.
* Les trois frères ibn Musa, Jafar, Ahmad, et Hasan (c. 800-?), membres de la bait al-hikma, mathématiciens et physiciens.
* Ahmed ibn Yusuf (835-912) alias al-Misri, égyptien, commente les livres 3 et 5 d'Euclide.
* al-Battani (c. 850-929), alias albategnius, fait des observations astronomiques à Antioche et ar-Raqqah en Syrie.
* Ibn Usayyid, chrétien vivant à Bagdad, élève de Thabit.
* Qusta ibn Luqa (870-912), traducteur en arabe de l'arithmétique de Diophante.
* abu Ishaq al-Sabi, haut fonctionnaire de Bagdad, ami d'al-Quhi.
* al-Uqlidisi (c. 920-c. 980), syrien, auteur d'un livre d'arithmétique contenant les chiffres indiens.
* al-Sijzi (c. 945-c. 1020), astronome perse.
* abu Nasr Mansur (970-1036), riche astronome ouzbek, disciple d'Abu'l-Wafa et maître d'al-Biruni.
* al-Biruni (973-1048), astronome ouzbek, voyage en Inde.
* al-Baghdadi alias Ibn Tahir (c. 980-1037), iraquien, s'établit comme professeur en Iran.
* ibn Sina, alias Avicenne (980-1037), médecin et philosophe perse.
* Nasir al-Tusi (1201-1274), perse, astronome à l'observatoire de Maragha, financé par Hulagu Khan petit-fils de Gengis Khan.
* ibn al-Banna (1256-1321), marocain, mathématicien complet, inventeur du mot almanach.
* al-Farisi (c. 1260-c. 1320) alias Kamal al-Din, perse, étudie l'arc en ciel et les nombres amicaux.
* al-Qalasadi (1412-1486), musulman espagnol, émigré en Afrique du nord, commentateur d'ibn al-Banna.Dernière modification par Invité, 21 août 2006, 13h09.
Commentaire
-
Al-Battani
Al-Battani (env. 855-923) était un astronome et mathématicien arabe (on écrit aussi Al Batani, et en latin : Albategnius, Albategni, Albatenius ; nom complet : Abū Abdullāh Muḥammad ibn Jābir ibn Sinān ar-Raqqī al-Ḥarrani aṣ-Ṣabiʾ al-Battānī ), né à Harran près d'Urfa. Son épithète as-Sabi suggère que ses ancêtres étaient membres de la secte des Sabéens qui adoraient les étoiles, mais son nom complet affirme qu'il était musulman. On le désigne parfois comme le Ptolémée des Arabes.
Al-Battani a travaillé en Syrie, à ar-Raqqah et à Damas où il est mort.
Son œuvre majeure, le Kitāb az-Zīj ( le « Livre des tables » ) composé de 57 chapitres, traduit en latin sous le titre de De Motu Stellarum par Platon de Tivoli (Plato Tiburtinus) en 1116 (imprimé en 1537 par Melanchthon, annoté par Regiomontanus), a considérablement influencé l'astronomie européenne. Une réédition apparut à Bologne en 1645. Le manuscrit original de Platon est conservé à la bibliothèque du Vatican. La bibliothèque de l'Escorial possède un manuscrit de chronologie astronomique d'al-Battani.
Astronomie
Il a corrigé certains calculs de Ptolémée et il a produit de nouvelles tables pour le Soleil et pour la Lune, qui ont longtemps fait autorité. Il a aussi traité la division de la sphère céleste. Il a découvert le mouvement de l'apogée du Soleil, calculé les valeurs de la précession des équinoxes ( 54.5" par an ) et l'inclinaison de l'axe terrestre ( 23° 35' ).
Mathématiques
Probablement sans connaître les travaux de l'astronome indien du Ve siècle Âryabhata , il a introduit l'usage du sinus dans les calculs, et en partie celui de la tangente, formant ainsi les bases de la trigonométrie moderne.
Il a utilisé les idées d'al-Marwazi sur les tangentes ( ou « ombres » ) pour développer des méthodes de calcul des tangentes et des cotangentes, et il en a dressé des tables.
Il a créé plusieurs formules trigonométriques :


Il a aussi résolu l'équation
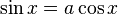
en la traduisant par l'équation suivante:
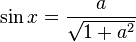
Commentaire
-
Al-Biruni
Abu Raihan Al-Biruni, aussi Alberuni arabe أبو الريحان البيروني persan ابوریحان بیرونی né le 15 septembre 973 - mort le 13 décembre 1048, était un mathématicien perse, un astronome, un physicien, un érudit, un encyclopédiste, un philosophe, un astrologue, un voyageur, un historien, un pharmacologue et un précepteur, originaire d'Asie centrale, qui contribua grandement aux domaines des mathématiques, philosophie, médecine et des sciences.
Il est né dans un faubourg de Kath, au Khwarezm, actuellement en Ouzbékistan, près de l'actuelle Ourguentch. Son nom vient du persan birun : extérieur, faubourg (de Kath). Son village a été renommé Beruni d'après lui. Il étudia les mathématiques et l'astronomie sous Abu Nasr Mansur.

Timbre soviétique commémorant le millénaire de la naissance d’al-Biruni.
Il fut un collègue du philosophe et médecin Ibn Sina, l'historien, philosophe et éthiciste Ibn Miskawayh, dans une université et un établissement de science établi par le prince Abu Al Abbas Ma'mun Khawarazmshah. Il voyagea aussi en Inde avec Mahmûd de Ghazni et l'accompagna dans sa campagne, apprenant la langue, et étudiant leur religion et leur philosophie, il écrivit un livre sur ses découvertes. Il connut aussi le grec, et probablement le syriaque et le berbère. Il écrivait ses livres en persan (sa langue natale) et en arabe.
Réalisations
Quelques unes de ses performances notables :
* À l'age de 17 ans, il calcula la latitude de Kath, au Khwarezm, utilisant l'altitude maximum du soleil.
* À 22 ans, il a écrit plusieurs ouvrages courts, incluant une étude sur les projections de cartes, Cartographie , qui inclut une méthodologie pour projeter un hémisphère sur un plan.
* À 27 ans, il a écrit un livre appelé Chronologie qui fait référence à un autre ouvrage qu'il a complèté (maintenant perdu) qui incluait plusieurs ouvrages dont un livre à propos de l'astrolabe, un à propos du système décimal, quatre à propos de astrologie, et deux à propos de l'histoire.
* Il calcula le rayon de la Terre à 6 339,6 km (ce résultat fut utilisé en occident au XVIe siècle).
Les travaux d'Al-Biruni s'élèvent à 120.
Ses contributions aux mathématiques incluent :
* L'arithmétique théorique et pratique
* La sommation des séries
* L'analyse combinatoire
* La règle de trois
* Les nombres irrationnels
* La théorie des rapports
* Les définitions algébriques
* Une méthode pour résoudre les équations algebriques
* La géométrie
* Les théorèmes d'Archimède
* La trisection de l'angle
Travaux

Illustration d’une éclipse de lune par al-Biruni.
Ses travaux non-mathématiques incluent :
* Étude des idées de l'Inde, qu'elles soient conformes à la raison ou rejetées par celle-ci, en arabe تحقيق ما للهند من مقولة معقولة في العقل أم مرذولة - Un compendium de la religion et de la philosophie de l'Inde.
* Les signes restants des siècles passés en arabe الآثار الباقية عن القرون الخالية - Une étude comparative des calendriers des différentes cultures et civilisations, mélées avec des informations mathématiques, astronomiques, et historiques.
* Le canon Mas'udi en arabe القانون المسعودي - Un livre à propos de l'astronomie, la géographie et l'ingénierie, en l'honneur de Mas'ud, fils de Mahmud de Ghazni, à qui il est dédicacé
* Comprendre l'astrologie en arabe التفهيم لصناعة التنجيم - Un livre en style question - réponse à propos des mathématiques et de l'astronomie, en arabe et en perse
* Pharmacologie - à propos des drogues et des médicaments
* Gemmes en arabe الجماهر في معرفة الجواهر à propos de la géologie, minéraux, et des gemmes, dédicacé à Mawdud fils de Mas'ud
* Astrolabe
* Un livre de résumé historique
* Une histoire de Mahmud de Ghazni et de son père
* Une histoire de Khawarazm
Commentaire
-
Thabit Ibn Qurra
Thabit Ibn Qurra, un des astronomes et des mathématiciens musulmans les plus célèbres et les plus en avant de sont temps à Bagdad. Al-Harrani d'Al-Sabi de Thabit Ibn Qurra Ibn Marwan est né en l'année 836 à Harran, il avécu en Turquie et en Irak.
La majorité de ses contributions se situent dans les mathématiques et l'astronomie. Il était instrumental et prolongea le concept de la géométrie traditionnelle à l'algèbre géométrique et a proposé plusieurs théories qui ont menées au développement de la géométrie non-Euclidienne, trigonométrie sphérique, calcul intégral et nombres réels.
Il a critiqué un certain nombre de théorèmes des éléments d'Euclide et a proposé des améliorations importantes. Il s'est appliqué la terminologie arithmétique aux quantités géométriques, et a étudié plusieurs aspects des sections coniques, notamment ceux de la parabole et ellipse. Un certain nombre de ses calculs ont visé à déterminer les surfaces et les volumes de différents types de corps et constituent, en fait, les processus du calcul intégral, comme développé plus tard.
Dans l'astronomie il était l'un des premiers réformateurs des vues de Ptoleme. Il a résolu beaucoup de problèmes liés aux mouvements du soleil et la lune et lui ont également écrit des livres sur des cadrans solaires.
Dans les domaines de la mécanique et de la physique il peut être identifié comme etablie la charge statique. Il a examiné des états de l'équilibre des corps, des faisceaux et des leviers. Non seulement il a traduit un grand nombre de livres lui-même, mais il a également fondé une école de traduction et a dirigé la traduction encore un autre de grand nombre de livres de grec à l'arabe.
Parmi les écritures de Thabit un grand nombre ont survécu, alors que plusieurs ne sont pas existants. La plupart des livres sont sur des mathématiques, suivies d'astronomie et de médecine. Les livres ont été écrits en arabe mais certains sont en Syriac, qui était le dialecte Aramaic oriental d'Odessa. Dans les âges moyens, Gherard de Crémone a traduit certains de ses livres en latin. Aux siècles récents, un certain nombre de ses livres ont été traduits en langues européennes et édités. Il a porté plus loin le travail des frères de Banu Musa et plus tard de son fils et fils continués dans cette tradition, avec l'aide d'autres membres du groupe. Au 9ème siècle son oeuvre originale comme ses traductions ont été une influence positive sur le développement de la recherche scientifique future.
Après une longue carrière, Thabit est mort à Bagdad dans 901 C.E.
Commentaire
-
Omar al-Khayyam
(wikipedia)
L'écrivain et savant persan Ghiyath ed-din Abdoul Fath Omar Ibn Ibrahim al-Khayyam Nishabouri, plus connu sous le nom d'Omar Khayyâm (farsi : غياث الدين ابو الفتح عمر بن ابراهيم خيام نيشابوري gīyath ad-dīn abū al-fath' umar ben ibrāhīm xayām nīšābūrī ou de Khayyam (du farsi: خيام en arabe : خَيَّميّ [xayyamī] : fabricant de tentes) serait né le 18 juin 1048 à Nichapur en Perse (actuel Iran) et mort le 4 décembre 1131.

Mausolée d'Omar Khayyam à Nichapur
Le nom de Khayyam
L'adoption du surnom persan Khayyam, fabricant de tentes est d'origine soufie. Si on le déchiffre avec le système abjad, le résultat donne al-Ghaqi, le dissipateur de biens, expression qui dans la terminologie soufie est attribuée à "celui qui distribue ou ignore les biens du monde constituant un fardeau dans le voyage qu'il entreprend sur le sentier soufi" (Omar Ali-Shah).
Le pacte de jeunesse
Trois étudiants de l'université de Nichapur conclurent un pacte à la fin de leurs études : « Celui d'entre nous qui atteindra la gloire ou la fortune devra partager à égalité avec les deux autres ». Tous trois atteignirent la notoriété par des voies différentes. Leurs noms étaient Ghiyath ed-din (Omar Khayyam), Abou-Ali-Hassan (Nizam al-Mulk) et Hassan ibn al-Sabbah. Les deux derniers se brouillèrent bien plus tard, mais leur protection s'étendit toujours sur Khayyam.
Abou-Ali-Hassan
Abou-Ali-Hassan (Nizam al-Mulk) fut le dernier grand vizir du sultan Alp Arslan. Conformément au pacte, il invita ses deux camarades à sa cour. Omar Khayyam, jusque-là étudiant, puis enseignant de mathématiques à Samarcande, se retrouva directeur de l'Observatoire à Ispahan.
Hassan ibn al-Sabbah
Hassan ibn al-Sabbah s'exila après quelque temps pour des raisons politiques et devint, sous le nom de Vieux de la Montagne, le chef d'une secte ismaelienne, la secte des Hashishins, tueurs dont le nom a donné le mot assassin (il faisait référence au hashish utilisé par eux). Ce groupe se livrait à des assassinats politiques. Hassan voulait faire "trembler les politiciens et les bases de ce monde", mais jamais Khayyam, malgré ses propos parfois quelque peu désinvoltes en matière religieuse, ne fut inquiété par elle : le pacte restait en vigueur. Nizam fut quant à lui assassiné par un membre de cette même secte. Elle exista à peu près 150 ans et ce fut les mongols lors de leur invasion de la Perse qui arrivèrent à finalement les éradiquer en détruisant leur forteresse principale, celle d'Alamut.
Cette légende doit être pondérée par le fait qu'Hassan ibn al-Sabbah avait environ 15 ans de moins que Khayyam, et Nizam al-Mulk environ 30 ans de plus.
Omar Khayyam, Hassan Sabbah, et Nizam El-MOlk, ne firent donc pas leurs études ensemble; Omar et Hassan sont en revanche originaires de la même ville, et se sont rencontrés que bien plus tard lors d'un voyage qu'il faisait tous les deux dans le but de rencontrer Nizam El-Molk. À la différence d'Hassan, Omar avait déjà rencontré une fois Nizam que celui-ci avait invité à venir le rejoindre.
Mathématicien et astronome
Dans ses Démonstrations de problèmes d'algèbre de 1070, Khayyam démontre que les équations cubiques peuvent avoir plus d’une racine. Il fait état aussi d’équations ayant deux solutions, mais n'en trouve pas à trois solutions.
Directeur de l'observatoire d'Ispahan en 1074, il réforme, à la demande du sultan Malik Shah, le calendrier persan. Il introduit une année bissextile et mesure la longueur de l’année comme étant de 365,24219858156 jours. Or la longueur de l’année change à la sixième décimale pendant une vie humaine. À la fin du XIXe siècle, l'année fait 365,242196 jours et aujourd’hui 365,242190 jours.
Khayyam découvre aussi le triangle de Pascal près de six siècles avant Blaise Pascal.
Commentaire
-
Al-Kachi
al-Kachi ou al-Kashi ("le natif de Kashan"), de son nom complet Ghiyath ad-Din Jamshid Mas`ud al-Kashi (ghiyâth ad-dîn : "secours de la religion", mas`ûd : "heureux" en arabe, ĵamšid : "Yama le brillant" en persan), mathématicien et astronome perse (vers 1380, Kashan (Iran) - 1429, Samarcande (Ouzbékistan)).

Ghiyath al-Din Jamshid Mas'ud al-Kashi, surnommé par un de ses pairs le nouveau Ptolémée, fut un mathématicien perse exceptionnel au moment de la Renaissance en Occident.
Biographie
Il assista à une éclipse de lune en 1406 à Kashan et rédigea plusieurs ouvrages astronomiques dans les années suivantes. Ses Khaqani zij (tables du grand khan) furent dédiées à Shah Rukh ou à Oulough Beg.
Oulough Beg invita al-Kashi à Samarcande en 1420, année de l'ouverture de la médersa qui porte son nom. Al-Kachi y enseigna avec Qadi-zadeh Roumi, le professeur d'Oulough Beg, et probablement Oulough Beg lui-même.
Al-Kachi joua un rôle important dans la conception de l'observatoire de Samarcande, inauguré vers 1429, et de ses instruments d'astronomie. Auparavant, les observations du ciel étaient réalisées à la médersa.
Les travaux menés par Oulough Beg, Qadi-zadeh Roumi, al-Kachi et quelque 60 autres savants aboutirent à la publication des Tables sultaniennes (zij-é solTâni, en persan), parues en 1437 mais améliorées par Oulough Beg jusque peu avant sa mort en 1449. Les données des Khaqani zij y furent bien sûr utilisées.
Des lettres écrites en persan par al-Kachi à son père décrivent en détail la vie scientifique à Samarcande à cette époque. Seuls Qadi-zadeh Roumi et Oulough Beg trouvent grâce à ses yeux. Al-Kachi était d'un tempérament peu raffiné, mais Oulough Beg le traitait avec bienveillance du fait de ses compétences.
Al-Kachi calcula le nombre π avec une précision de 15 décimales, qui devait rester inégalée pendant près de deux siècles.
Théorème d'Al-Kashi
Le théorème d'Al-Kashi est un théorème de géométrie du triangle couramment utilisé en trigonométrie. Il généralise le théorème de Pythagore aux triangles non rectangles : il relie le troisième côté d'un triangle aux deux premiers ainsi qu'au cosinus de l'angle formé par ces deux côtés.
Soit un triangle ABC

dans lequel on utilise les notations : d'une part α, β et γ pour les angles et, d'autre part, a, b et c pour les côtés respectivement opposés à ces angles. Alors, le théorème d'al-Kashi stipule que :

Dans la plupart des autres langues, ce théorème est connu sous le nom de loi des cosinus, appellation toutefois relativement tardive. En français, cependant, il porte le nom du mathématicien perse Ghiyath al-Kashi qui unifia les résultats de ses prédécesseurs.
Commentaire
-
Salut far solitaire
disons que j'ai un peu abondonné FA ,c'est des periode!!!mais la je suis de retour..Hey lila, ça fait un bail, t'était en vacance ?
et toi toujous là à nous imprégner de ta vaste culture
au fait merci pour la biographie de Omar al-khayyam c'est vraiment un des savants de l'époque que j'apprécie le plus , j'ai eu l'occasion à travers Samarcande d'amin maalouf d'y découvrir sa personnalité si tu ne la pas encore lu je te le conseille ....
Commentaire
-
Un Ouled Houmti
Born: 29 Dec 1256 in Marrakesh, Morocco
Died: 1321 in Marrakesh, Morocco
Ibn al-Banna is also known as Abu'l-Abbas Ahmad ibn Muhammad ibn Uthman al-Azdi. It is a little unclear whether al-Banna was born in the city of Marrakesh or whether it was the region of Marrakesh which was named Morocco by Europeans. There is a claim that al-Banna was born in Granada in Spain and moved to North Africa for his education. What is certain is that he spent most of his life in Morocco.
The Marinids tribe were allies of the Umayyad caliphs of Córdoba. The tribe lived in eastern Morocco then, under their ruler Abu Yahya, they began to conquer the region. The Marinids captured Fez in 1248 and made it their capital. They captured Marrakesh from the ruling Almohads tribe in 1269, thus taking control of the whole of Morocco. Having conquered Morocco, the Marinids tried to help Granada to prevent the Christian advance through their country. The strong link between Granada and Morocco may account for the confusion as to which country al-Banna was a native.
Morocco was certainly the country that al-Banna was educated in, learning the leading mathematical skills of the period. He studied geometry in general, and Euclid's Elements in particular. He also studied fractional numbers and learnt much of the impressive contributions that the Arabs had made to mathematics over the preceding 400 years. The Marinids had a strong culture for learning and Fez became their centre of learning. At the university in Fez Al-Banna taught all branches of mathematics, which at this time included arithmetic, algebra, geometry and astronomy. Fez was a thriving city with a new quarter being built housing the Royal Palace and the adjoining Great Mosque. Many students studied under al-Banna in this thriving academic community.
It is clear that al-Banna wrote a large number of works, in fact 82 are listed by Renaud (see for example [9]). Not all are on mathematics, but the mathematical texts included an introduction to Euclid's Elements, an algebra text and various works on astronomy. One difficulty with the works on mathematics is knowing how much of the material which al-Banna presents is original and how much is simply his version of work by earlier Arab mathematicians which has been lost. We should certainly say that al-Banna does not claim any originality and, indeed, the style of his writing would suggest that he is collecting together ideas that he has learnt from other mathematicians.
Two "firsts" for al-Banna are that he seems to have been the first to consider a fraction as a ratio between two numbers (see [12] for more details) and he is the first to use the expression almanakc (in Arabic al-manakh meaning weather) in a work containing astronomical and meteorological data.
Perhaps al-Banna's most famous work is Talkhis amal al-hisab (Summary of arithmetical operations) and the Raf al-Hijab which is al-Banna's own commentary on the Talkhis amal al-hisab. It is in this work that al-Banna introduces some mathematical notation which has led certain authors to believe that algebraic symbolism was first developed in Islam by ibn al-Banna and al-Qalasadi (see for example [6]). We refer the reader to the biography of al-Qalasadi where we present arguments to show that neither al-Banna nor al-Qalasadi were the inventors of mathematical notation.
There are, however, many interesting mathematical ideas and results which appear in the Raf al-Hijab. For example it contains continued fractions and they are used to compute approximate square roots. Other interesting results on summing series are the results
13 + 33 + 53 + ... + (2n-1)3 = n2(2n2 - 1) and
12 + 32 + 52 + ... + (2n-1)2 = (2n + 1)2n(2n - 1)/6.
Perhaps the most interesting of all is the work on binomial coefficients which is described in detail in [2] and [3]. If we denote the binomial coefficient p choose k by pCk then al-Banna shows that
pC2 = p(p-1)/2
and then that
pC3 = pC2(p-2)/3.
He writes (see for example [2] or [3]):-
... the ternary combination is thus obtained by multiplying the third of the third term preceding the given number; and so we always multiply the combination that precedes the combination sought by the number that precedes the given number, and whose distance to it is equal to the number of combinations sought. From the product, we take the part that names the number of combinations.
Although this is a little difficult to interpret, what al-Banna is stating here is that
pCk = pCk-1(p - (k - 1) )/k.
He then goes on to give the familiar (to us) result
pCk = p(p - 1)(p - 2)...(p - k + 1)/(k !)
As Rashed points out in [2], this is only a small step from the Pascal triangle results given three hundred years earlier by al-Karaji, then still one hundred years before al-Banna by al-Samawal. However Rashed writes:-
... in our opinion, there is something more fundamental than [the Pascal triangle] results; it is precisely the combinatorial appearance of ibn al-Banna's exposition, together with the relation he partially establishes between polygonal numbers and combinations. It concern, in the first place, triangular numbers and combinations of p objects in twos, and then polygonal numbers of order 4 and combinations of p objects in threes.
Article by: J J O'Connor and E F Robertson
Source: MacTutor History of Mathematics
References for Ibn al-Banna
Biography in Dictionary of Scientific Biography (New York 1970-1990)
Books:
1-R Rashed, The development of Arabic mathematics : between arithmetic and algebra (London, 1994).
2-R Rashed, Entre arithmétique et algèbre: Recherches sur l'histoire des mathématiques arabes (Paris, 1984).
Articles:
1-M Aballagh, Les fondements des mathématiques à travers le 'Raf al-Hijab' d'Ibn al-Banna (1256-1321), in Histoire des mathématiques arabes, Algiers, 1986 (Algiers, 1988), 133-156.
2-M Aballagh, Les fractions entre la théorie et la pratique chez Ibn al-Banna al-Murrakusi (1256-1321), in Histoire de fractions, fractions d'histoire (Basel, 1992), 247-258; 405-406; 411.
3-G Arrighi, Review of some mathematical symbols (Italian), Physis - Riv. Internaz. Storia Sci. 27 (1-2) (1985), 163-179.
4-A Djebbar, Enseignement et recherche mathématiques dans le Maghreb des XIIIe-XIVe siècles : étude partielle (Orsay, 1981).
5-R Rashed, Materials for the study of the history of amicable numbers and combinatorial analysis (Arabic), J. Hist. Arabic Sci. 6 (1-2) (1982), 278-209.
6-H P J Renaud, Ibn al-Banna de Marrakech, sufi et mathématicien, Hesperis 25 (1938), 13-42.
7-H P J Renaud, Sur les dates de la vie du mathématicien arabe marocain Ibn al-Banna, Isis 27 (1937), 216-218.
8-J Samsó and E Millás, The computation of planetary longitudes in the zij of Ibn al-Banna, Arabic Sci. Philos. 8 (2) (1998), 165; 167; 259-286.
9-M Zarruqi, Fractions in the Morroccan mathematical tradition between the 12th and 15th centuries A.D. as found in anonymous manuscripts (Arabic), in Deuxième Colloque Maghrebin sur l'Histoire des Mathématiques Arabes (Tunis, 1990), A97-A109.
Commentaire

 j'y reviendrai après, notamment aux mathématiciens arabes et perses suivants :
j'y reviendrai après, notamment aux mathématiciens arabes et perses suivants :
Commentaire