Fibonacci et l'école Bejaia
Leonardo Fibonacci (Pise, v. 1170 - v. 1250) est un mathématicien italien. Fibonacci (de son nom moderne), connu à l'époque sous le nom de Leonardo Pisano (Léonard de Pise), mais aussi de Leonardo Bigollo (bigollo signifiant voyageur), s'appelait en réalité Leonardo Guilielmi.

Né à Pise, en Italie, son éducation s'est faite en grande partie en Afrique du Nord. Son père, Guilielmo Bonacci, gérait les marchés de la république de Pise en Algérie, en Tunisie et au Maroc… Il en rapporta, dit-on, en 1200, les chiffres arabes et la notation algébrique, dont d'autres attribuent l'introduction à Gerbert d'Aurillac. En 1202, il publie son Liber Abaci, un traité sur les calculs et la comptabilité. Ce dernier est fortement influencé par sa vie dans les pays arabes ; il est d'ailleurs rédigé en partie de droite à gauche. Par cette publication, Fibonacci introduit le système de notation arabo-indien en Europe. Ce système est bien plus puissant que la notation romaine, et Fibonacci en est pleinement conscient. Il peina cependant à s'imposer avant plusieurs siècles.
Le célèbre "Dictionary of scientific biography" le présente comme le premier grand mathématicien de l'Occident chrétien.
Dans son important ouvrage, Le Liber Abaci, il dit lui même qu'il a étudié la science du calcul et l'algèbre d'al-Khawarismi à Béjaia auprès d'un maître admirable ("exmirabili magisterio").
il y appris "le maniement de l'abaque, en même temps que celui des chiffres arabes, la façon d'apprécier la valeur d'une monnaie d'aprés la quantité de fin..".
Cet évènement permettra le début d'une ère nouvelle en Occident. En effet, l'activité créatrice dans le domaine des mathématiques va renaître grâce à l'initiation des savants italiens aux méthodes de calcul des Pays de l'Islam.
Le Liber Abaci
Le Liber Abaci a été publié en 1202. il s'agit d'un traité d'arithmétique qui prône les avantages de la méthode positionnelle indienne. Les démonstrations reposent sur des arguments géométriques empruntés à Euclide car, comme Fibonacci le signale, arithmétique et géométrie s'interprètent et se viennent mutuellement en aide.
L'ouvrage se veut didactique et est divisé en quinze chapitres.
Le chapitre 1 traite de la connaissance des neuf figures indiennes ainsi que du zéro qui indique q'une position est "vacante".
les autres chapitres traitent de la multiplication des entiers, addition, soustraction, division, multiplication des fractions et des entiers , calcul des prix, applications commerciales (alliages et monnaies), progressions et proportions, règles de fausses positions, calcul à effectuer avec des radicaux carrés et cubiques (il est donc dans la tradition du livre X d'Euclide).
Enfin, le dernier chapitre est consacré à des problèmes numériques de géométrie et à la résolution des équations du second degré, suivant les méthodes d'al-Khawarizmi (mort en 850).
Les mathématiques à Bougie et Fibonacci
Le haut niveau des enseignements mathématiques qui y dispensés est notamment attesté par le cour d'algèbre supérieure d'al-Qurashi.
Ce dernier, qui a vécu à Bougie ers la fin du XII-ème siècle (aanr le séjour de Fibonacci), aurait rédigé l'un des meilleurs commentaires du traité d'algèbre du célèbre mathématicien égyptien Abu Kamil sur les six équations [canoniques]. Or, l'influence d'Abu Kamil sur l'œuvre de Fibonacci a été soulignée par plusieurs auteurs(cf. les travaux de S. Chelboub et de André Allard).
En ce qui concerne le "maître admirable"de Fibonacci, aucun élément ne permet de l'identifier.
On peut néanmoins faire certaines hypothèses en se basant sur la structuration du milieu scientifique (voir figure1 [Aissani 1994]). La plus probable est qu'il ait appartenu au groupe du mathématicien al-Usili.
l'appartenance aux groupes des andalous et de la Qal'a est également possible (Ibn Hammad avait dépassé la quarantaine au moment du séjour de Fibonacci).
Par ailleurs, rappelons que l'utilisation d'un certain symbolisme pour exprimer les concepts essentiels était l'une des principales caractéristiques de l'enseignement mathématique dans le nord de l'Afrique au Moyen age. Or, le genre de symboles que l'on retrouve déjà au XII-éme siècle chez le mathématicien Maghrébin al-Hassar (qui était la référence à Bougie (cf. le témoignage du bio-bibliographe al-Gubrini) semble avoir joué chez
Léonard de Pise un certain rôle (cf. l'exemple des fraction continue ascendantes- Léonard les appelle "fractiones in gradibus", fractions en degrés).
Mathématiques commerciales
Tous les historiens reconnaissent aujourd'hui le rôle historique joué par les marchands dans la transmission de la culture mathématique . Cette dernière a ouvert des voies nouvelles dans la façon de penser la science, autrement dit, de préparer l'ère moderne.
On retrouve dans le liber Abaci de nombreuses applications de l'arithmétique opératoire au commerce:calcul des prix, trocs et ristournes, règle de société, problème de change (alliages et monnaies).
L'équivalence des mesures entre Bougie, Pise et Gênes y est traitée. à ce propos un autre opscule d'usage courant illustre l'équivalence entre les différents systèmes du "contare" en usage à Bougie, à Pise et à Gêne. Il s'agit du mémoria de 1278 (qui est d'un auteur inconnu).
Fibonacci aujourd'hui
Les travaux de Léonardo Fibonacci continuent plus que jamais d'inspirer les mathématiciens du monde entier. Ainsi, du 24 au 28 Juin 2002 se déroulera en Arizona (U.S.A) la Dixième Conférence Internationale sur les Nombres de Fibonacci et ses Applications (voir présentation dans les Notices de l'American Mathematical Society, Vol. 48,n°9, October 2001, p.1050). Par ailleurs, il existe une fondation internationale, The Fibonacci Association qui édite aux États Unis une revue internationale de très haut niveau, "The Fibonacci Quarterly" . Parmi les applications significatives, citons cet exemple tiré de la finance : convaincu que les cours de la bourse suivent un ordre naturel, Ralph Nelson Elliot (1871 - 1948) intégra les nombres de Fibonacci à sa théorie des vagues.
Suite de Fibonacci
La célèbre suite de Fibonacci doit son nom au mathématicien italien Leonardo Pisano, mieux connu sous le pseudonyme de Fibonacci (1170 - 1250). Dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, il décrit la croissance d'une population de lapins :
« Possédant initialement un couple de lapins, combien de couples obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? »
Ce problème est à l'origine de la suite de Fibonacci, dont le n'ème terme correspond au nombre de paires de lapins au n'ème mois. Dans cette population (idéale), on suppose que :
* le premier mois, il y a juste une paire de lapereaux ;
* les lapereaux ne sont pubères qu'à partir du deuxième mois ;
* chaque mois, toute paire susceptible de procréer engendre effectivement une nouvelle paire de lapereaux ;
* les lapins ne meurent jamais (ie. la suite de Fibonacci est strictement croissante).
la forme récurrente de la suite de Fibonacci est :
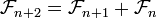
Son expression fonctionnelle, laquelle porte le nom de formule de Binet est :

Les termes de cette suite sont appelés nombres de Fibonacci. En voici quelques-uns dans l'ordre croissant :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
(wikipedia et gehimab.org)
Leonardo Fibonacci (Pise, v. 1170 - v. 1250) est un mathématicien italien. Fibonacci (de son nom moderne), connu à l'époque sous le nom de Leonardo Pisano (Léonard de Pise), mais aussi de Leonardo Bigollo (bigollo signifiant voyageur), s'appelait en réalité Leonardo Guilielmi.

Né à Pise, en Italie, son éducation s'est faite en grande partie en Afrique du Nord. Son père, Guilielmo Bonacci, gérait les marchés de la république de Pise en Algérie, en Tunisie et au Maroc… Il en rapporta, dit-on, en 1200, les chiffres arabes et la notation algébrique, dont d'autres attribuent l'introduction à Gerbert d'Aurillac. En 1202, il publie son Liber Abaci, un traité sur les calculs et la comptabilité. Ce dernier est fortement influencé par sa vie dans les pays arabes ; il est d'ailleurs rédigé en partie de droite à gauche. Par cette publication, Fibonacci introduit le système de notation arabo-indien en Europe. Ce système est bien plus puissant que la notation romaine, et Fibonacci en est pleinement conscient. Il peina cependant à s'imposer avant plusieurs siècles.
Le célèbre "Dictionary of scientific biography" le présente comme le premier grand mathématicien de l'Occident chrétien.
Dans son important ouvrage, Le Liber Abaci, il dit lui même qu'il a étudié la science du calcul et l'algèbre d'al-Khawarismi à Béjaia auprès d'un maître admirable ("exmirabili magisterio").
il y appris "le maniement de l'abaque, en même temps que celui des chiffres arabes, la façon d'apprécier la valeur d'une monnaie d'aprés la quantité de fin..".
Cet évènement permettra le début d'une ère nouvelle en Occident. En effet, l'activité créatrice dans le domaine des mathématiques va renaître grâce à l'initiation des savants italiens aux méthodes de calcul des Pays de l'Islam.
Le Liber Abaci
Le Liber Abaci a été publié en 1202. il s'agit d'un traité d'arithmétique qui prône les avantages de la méthode positionnelle indienne. Les démonstrations reposent sur des arguments géométriques empruntés à Euclide car, comme Fibonacci le signale, arithmétique et géométrie s'interprètent et se viennent mutuellement en aide.
L'ouvrage se veut didactique et est divisé en quinze chapitres.
Le chapitre 1 traite de la connaissance des neuf figures indiennes ainsi que du zéro qui indique q'une position est "vacante".
les autres chapitres traitent de la multiplication des entiers, addition, soustraction, division, multiplication des fractions et des entiers , calcul des prix, applications commerciales (alliages et monnaies), progressions et proportions, règles de fausses positions, calcul à effectuer avec des radicaux carrés et cubiques (il est donc dans la tradition du livre X d'Euclide).
Enfin, le dernier chapitre est consacré à des problèmes numériques de géométrie et à la résolution des équations du second degré, suivant les méthodes d'al-Khawarizmi (mort en 850).
Les mathématiques à Bougie et Fibonacci
Le haut niveau des enseignements mathématiques qui y dispensés est notamment attesté par le cour d'algèbre supérieure d'al-Qurashi.
Ce dernier, qui a vécu à Bougie ers la fin du XII-ème siècle (aanr le séjour de Fibonacci), aurait rédigé l'un des meilleurs commentaires du traité d'algèbre du célèbre mathématicien égyptien Abu Kamil sur les six équations [canoniques]. Or, l'influence d'Abu Kamil sur l'œuvre de Fibonacci a été soulignée par plusieurs auteurs(cf. les travaux de S. Chelboub et de André Allard).
En ce qui concerne le "maître admirable"de Fibonacci, aucun élément ne permet de l'identifier.
On peut néanmoins faire certaines hypothèses en se basant sur la structuration du milieu scientifique (voir figure1 [Aissani 1994]). La plus probable est qu'il ait appartenu au groupe du mathématicien al-Usili.
l'appartenance aux groupes des andalous et de la Qal'a est également possible (Ibn Hammad avait dépassé la quarantaine au moment du séjour de Fibonacci).
Par ailleurs, rappelons que l'utilisation d'un certain symbolisme pour exprimer les concepts essentiels était l'une des principales caractéristiques de l'enseignement mathématique dans le nord de l'Afrique au Moyen age. Or, le genre de symboles que l'on retrouve déjà au XII-éme siècle chez le mathématicien Maghrébin al-Hassar (qui était la référence à Bougie (cf. le témoignage du bio-bibliographe al-Gubrini) semble avoir joué chez
Léonard de Pise un certain rôle (cf. l'exemple des fraction continue ascendantes- Léonard les appelle "fractiones in gradibus", fractions en degrés).
Mathématiques commerciales
Tous les historiens reconnaissent aujourd'hui le rôle historique joué par les marchands dans la transmission de la culture mathématique . Cette dernière a ouvert des voies nouvelles dans la façon de penser la science, autrement dit, de préparer l'ère moderne.
On retrouve dans le liber Abaci de nombreuses applications de l'arithmétique opératoire au commerce:calcul des prix, trocs et ristournes, règle de société, problème de change (alliages et monnaies).
L'équivalence des mesures entre Bougie, Pise et Gênes y est traitée. à ce propos un autre opscule d'usage courant illustre l'équivalence entre les différents systèmes du "contare" en usage à Bougie, à Pise et à Gêne. Il s'agit du mémoria de 1278 (qui est d'un auteur inconnu).
Fibonacci aujourd'hui
Les travaux de Léonardo Fibonacci continuent plus que jamais d'inspirer les mathématiciens du monde entier. Ainsi, du 24 au 28 Juin 2002 se déroulera en Arizona (U.S.A) la Dixième Conférence Internationale sur les Nombres de Fibonacci et ses Applications (voir présentation dans les Notices de l'American Mathematical Society, Vol. 48,n°9, October 2001, p.1050). Par ailleurs, il existe une fondation internationale, The Fibonacci Association qui édite aux États Unis une revue internationale de très haut niveau, "The Fibonacci Quarterly" . Parmi les applications significatives, citons cet exemple tiré de la finance : convaincu que les cours de la bourse suivent un ordre naturel, Ralph Nelson Elliot (1871 - 1948) intégra les nombres de Fibonacci à sa théorie des vagues.
Suite de Fibonacci
La célèbre suite de Fibonacci doit son nom au mathématicien italien Leonardo Pisano, mieux connu sous le pseudonyme de Fibonacci (1170 - 1250). Dans un problème récréatif posé dans un de ses ouvrages, le Liber Abaci, il décrit la croissance d'une population de lapins :
« Possédant initialement un couple de lapins, combien de couples obtient-on en douze mois si chaque couple engendre tous les mois un nouveau couple à compter du second mois de son existence ? »
Ce problème est à l'origine de la suite de Fibonacci, dont le n'ème terme correspond au nombre de paires de lapins au n'ème mois. Dans cette population (idéale), on suppose que :
* le premier mois, il y a juste une paire de lapereaux ;
* les lapereaux ne sont pubères qu'à partir du deuxième mois ;
* chaque mois, toute paire susceptible de procréer engendre effectivement une nouvelle paire de lapereaux ;
* les lapins ne meurent jamais (ie. la suite de Fibonacci est strictement croissante).
la forme récurrente de la suite de Fibonacci est :
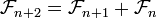
Son expression fonctionnelle, laquelle porte le nom de formule de Binet est :

Les termes de cette suite sont appelés nombres de Fibonacci. En voici quelques-uns dans l'ordre croissant :
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, ...
(wikipedia et gehimab.org)

Commentaire